미니맥스 알고리즘
알파베타 가지치기 알고리즘
게임의 조건
게임을 위한 프로그램을 작성하는 문제를 생각해 보자. 설명을 단순화하기 위해 우리는 다음과 같은 속성을 가진 게임만 고려할 것이다.
바둑이나 체스가 여기에 속한다.
- 두 명의 경기자 - 경기자들이 연합하는 경우는 다루지 않는다.
- 제로썸 게임 - 한 경기자의 승리는 다른 경기자의 패배다. 협동적인 승리는 없다.
- 차례대로 수를 두는 게임만을 대상으로 한다.(순차적인 게임)
인공지능과 게임
게임은 예전부터 인공지능의 매력적인 연구 주제였다.
Tic-Tac-Toe나 체스, 바둑과 같은 게임은 추상적으로 정의할 수 있고 지적 능력과 연관이 있는 것으로 생각되었다.
이들 게임은 비교적 적은 수의 연산자들을 가진다. 연산의 결과는 엄밀한 규 칙으로 정의된다.
바둑에서 나타나는 모든 경우의 수
바둑판에는 돌을 놓을 수 있는 곳이 19×19=361이다. 한 곳에는 흰돌(white) 또는 검은돌(black) 또는 비워놓을 수 있다(empty). 따라서 각 361개의 점마 다 최대 3가지의 선택이 있다. 따라서 발생할 수 있는 상태의 상한은 다음과 같다.
3 × 3 × 3 × ... = 3^361
2.1×10^170 정도의 숫자라고 한다. 이것은 엄청난 숫자로써 우주에 존재하는 원자의 개수로 믿어지는 숫자인 1080보다도 훨씬 많다. 따라서 효율적 탐색 이 필요하다.
게임의 정의
- 2인용 게임
- 두 경기자를 MAX와 MIN으로 부르자.
- 항상 MAX가 먼저 수를 둔다고 가정한다.
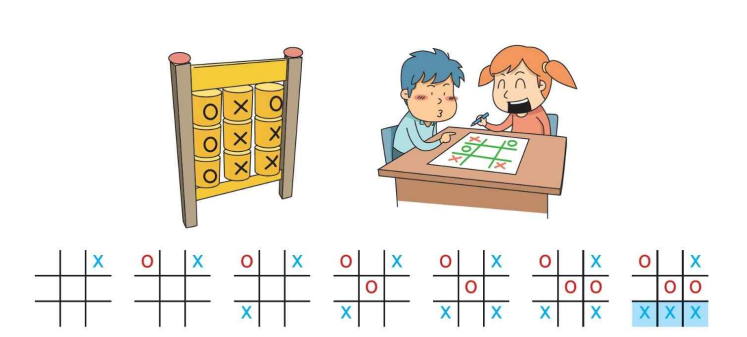
Tic-Tac-Toe의 게임 트리

Tic-Tac-Toe 게임 트리의 크기
Tic-Tac-Toe의 게임 트리는 크기가 얼마나 될까?
Tic-Tac-Toe 게임 보드는 3×3 크기를 가지고 있고 한 곳에 수를 놓으면 다른 사람이 놓을 수 있는 곳은 하나가 줄어들게 된다. 9×8×7×...×1 = 9! = 362,880
미니맥스 알고리즘
안전하게 하려면 상대방이 최선의 수를 둔다고 생각하면 된다.
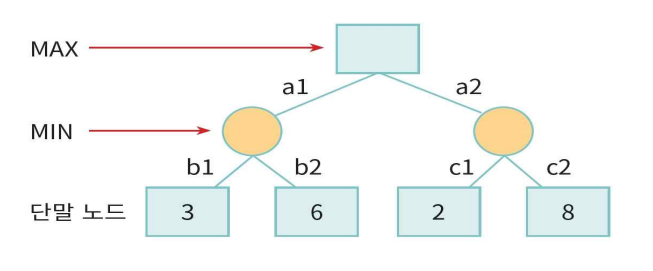
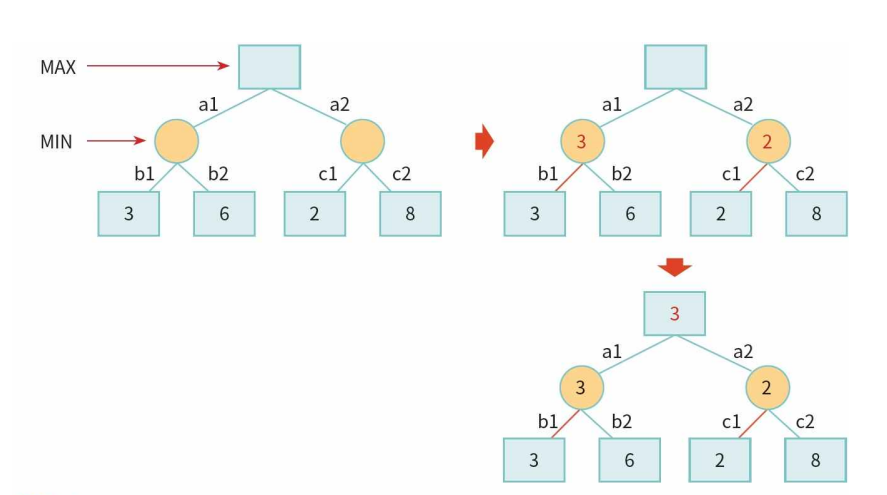
평가값이 높으면 MAX 유리, 낮으면 MIN 유리
미니맥스(minimax) 알고리즘
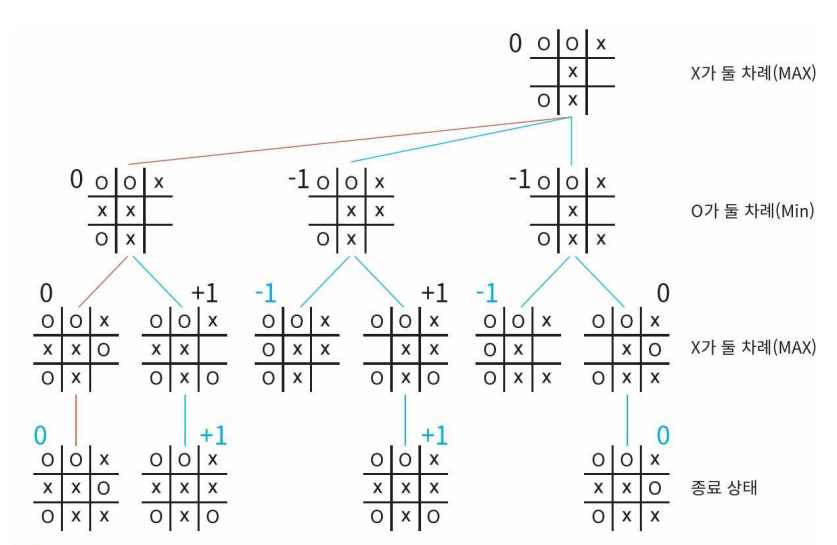
틱택토 게임에서의 미니맥스
미니맥스 알고리즘 실습
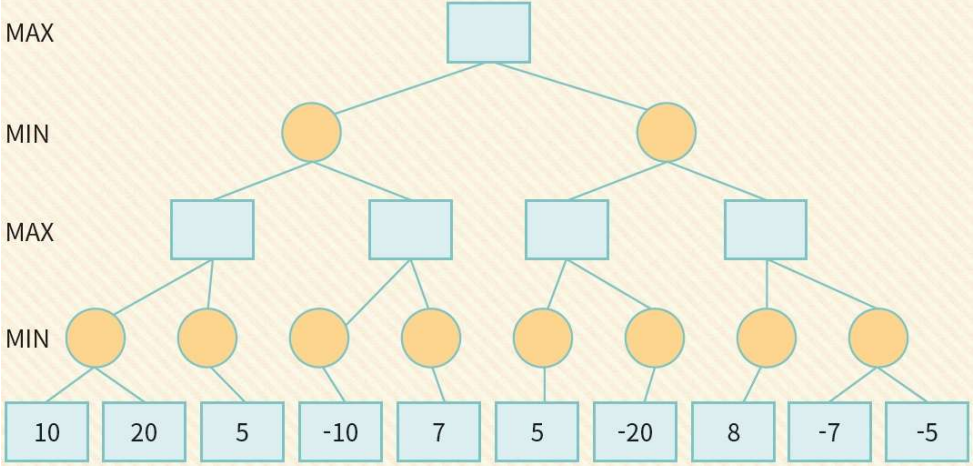
미니맥스 알고리즘의 분석
- 완결성: 미니맥스 알고리즘은 완결될 수 있다. 유한한 탐색 트리 안에 해답이 존재하면 반드시 찾는다.
- 최적성: 미니맥스 알고리즘은 최적의 알고리즘이다.
- 시간 복잡도: 만약 트리의 최대 깊이가 m이고 각 노드에서의 가능한 수가 b 개라면, 미니맥스 알고리즘의 시간 복잡도는 O(b^m)이다.
- 공간 복잡도: 공간 복잡도도 O(b^m) 이다.
알파베타 가지치기
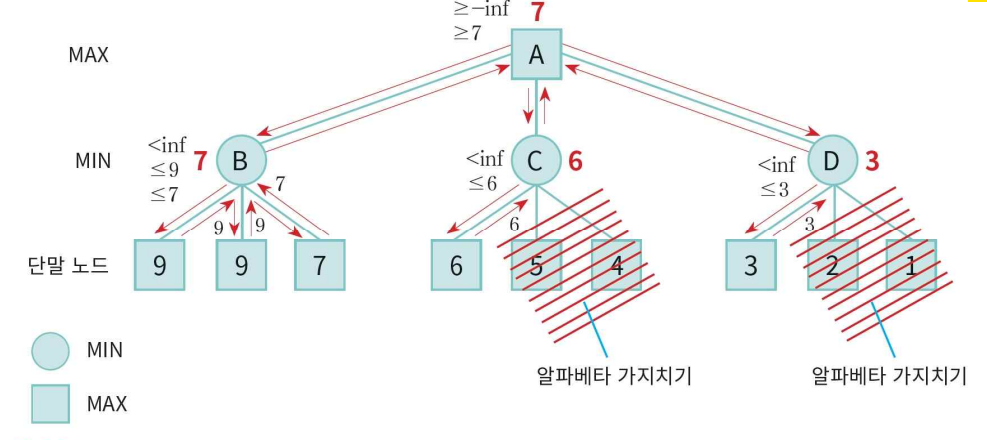
- B의 왼쪽노드 9이므로 최소화 노드인 B는 적어도 9보다 같거나 작아짐
- B의 중간노드 9이므로 최소화 노드인 B는 적어도 9보다 같거나 작아짐
- B의 오른쪽노드 7이므로 최소화 노드인 B는 적어도 7보다 같거나 작아짐
- B 평가값은 7이 되고, 노드 A로 전달. A는 최대화 노드로서 7보다 같거나 커짐
- C 왼쪽노드 6이므로 최소화 노드인 C는 6보다 같거나 작아짐. 자식노드 C가 아무리 커져봐야 6이면 더 이상 탐색 무의미. C 나머지 탐색 중단
미니매스 알고리즘에서 형성되는 탐색 트리 중에서 상당 부분은 결과에 영 향을 주지 않으면서 가지들을 쳐낼 수 있다.
이것을 알파베타 가지치기라고 한다.
탐색을 할 때 알파값과 베타값이 자식 노드로 전달된다. 자식 노드에서는 알 파값과 베타값을 비교하여서 쓸데없는 탐색을 중지할 수 있다.
MAX는 알파값만을 업데이트한다. MIN은 베타값만을 업데이트한다.

- 노드A의 α는 -∞이고 β는 +∞로 설정. 이 값은 후속 노드로 전달.
- A는 최대화 노드이므로 B,C 중에서 최대값 노드 선택.
- B는 최소화 노드이므로 D,E 중에서 최소값 노드 선택.
- 노드 D에서 왼쪽 노드값이 4이므로 α는 max(-∞,4)로 4가 됨.
- α ≥β이면 가지치기 가능. 4 ≥ +∞ 아니므로 탐색
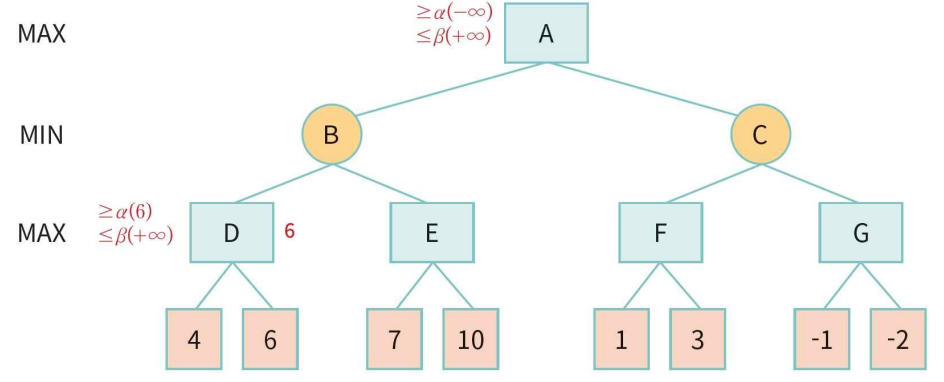
- 노드D의 오른쪽 자식. 노드값이 6이므로 α= max(4,6) =6. 노드 D평가값=6
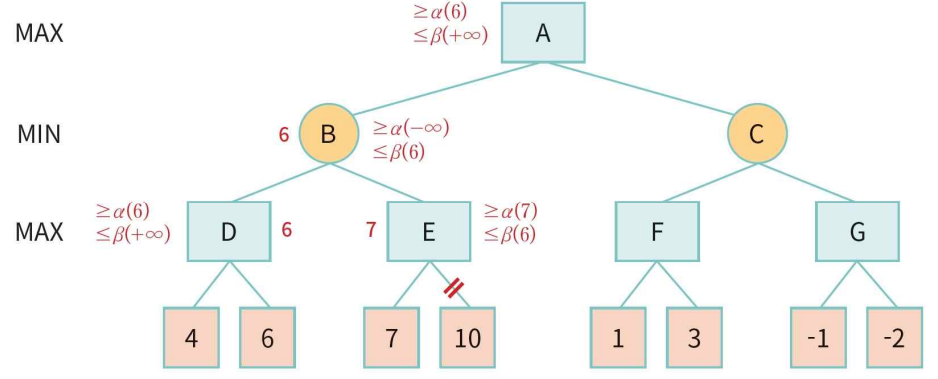
- 노드 D는 노드 B로 6의 값 반환. B에서 β =min(+∞ ,6)=6.
- 노드 B는 6 또는 더 낮은 값 보장.
- B는 E 를 호출하여 6보다 낮은 값을 얻을 수 있는지 확인.
- 노드 E에서 α=-∞, β =6 전달.
- E는 왼쪽 자식 7. α=max(-∞,7)=7. α≥β 조건이 참. 더 이상 자식노드 10 탐색안하고 7 반환.
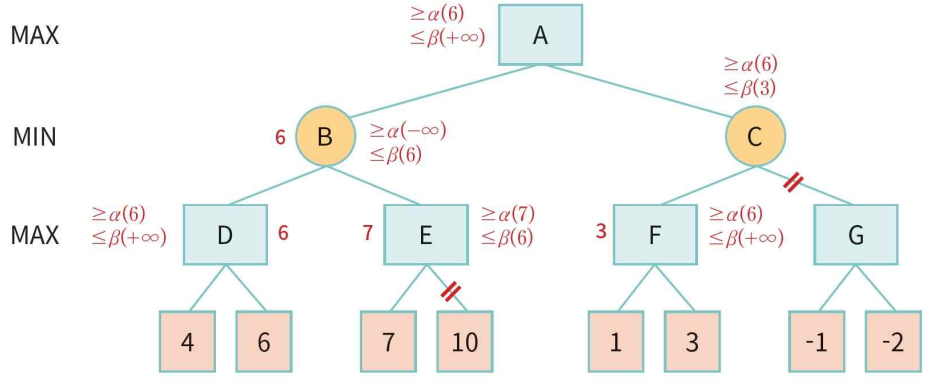
- 노드 B에서 β =min(6,7)=6. 6의 값 노드 A로 반환. A에서 α=max(-∞,6)=6
- 노드 A는 6 보다 큰 값을 가질 수 있다는 것이 보장.
- C는 α=6, β=+∞, 이 값으로 F호출.
- F 왼쪽 자식 1, F에서 α=max(6,1)=6.
- F 오른쪽 자식 3, 따라서 F는 3이고 α는 변경 없음.
- F의 값 3이 C로 반환. C 에서 β =min(+∞,3)=3. α≥β 조건이 참. C오른쪽 G 탐색안함.
불완전한 결정
- 미니맥스 알고리즘은 탐색 공간 전체를 탐색하는 것을 가정한다. 하지만 실 제로는 탐색 공간의 크기가 무척 커서 우리는 그렇게 할 수 없다. 실제로는 적당한 시간 안에 다음 수를 결정하여야 한다. 어떻게 하면 될까?
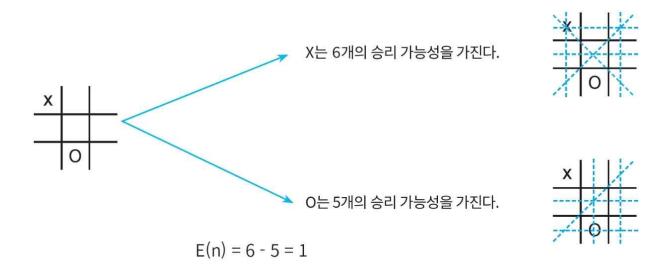
- 이때는 탐색을 끝내야 하는 시간에 도달하면 탐색을 중단하고 탐색 중인 상 태에 대하여 휴리스틱 평가 함수(evaluation function)를 적용해야 한다. 즉 비단말 노드이지만 단말 노드에 도달한 것처럼 생각하는 것이다.
- 평가함수 예: 승리상태>무승부상태>패배상태 순으로 추정치가 높도록
요약
- 게임에서는 상대방이 탐색에 영향을 끼친다. 이 경우에는 미니맥스 알고리 즘을 사용하여 탐색을 진행할 수 있다. 미니맥스 알고리즘은 상대방이 최선 의 수를 둔다고 가정하는 알고리즘이다.
- 두 명의 경기자 MAX와 MIN이 있으며, MAX는 평가 함수값이 최대인 자식 노드를 선택하고 MIN은 평가 함수값이 최소인 자식 노드를 선택한다.
- 탐색 트리의 어떤 부분은 제외하여도 결과에 영향을 주지 않는다. 이것을 알 파베타 가지치기(alpha-beta pruning)라고 한다.
'끝이없는 공부 > 인공지능개론' 카테고리의 다른 글
| [인공지능개론] 6장. 퍼지논리 (1) | 2024.05.08 |
|---|---|
| [인공지능개론] 5장. 지식표현 (0) | 2024.05.07 |
| [인공지능개론] 4장. 전문가시스템 (0) | 2024.05.01 |
| [인공지능개론] 2장. 탐색 (0) | 2024.04.19 |
| [인공지능개론] 1장. 인공지능 소개 (0) | 2024.04.19 |



