728x90
반응형
여러가지 지식표현 방법
술어논리 이해
술어논리에서 사용되는 추론기법 이해
지식표현 방법

지식 표현 모델의 분류
| 지식 표현 모델 | 종류 |
| 생성 규칙(Production Rule) 또는 규칙 | 절차적(procedural) |
| 술어논리(Predicate Logic) | 선언적(declarative) |
| 의미망(Semantic Net) | 선언적(declarative) |
| 프레임(Frame) | 선언적(declarative) |
규칙
- 규칙은 전제(IF문)와 결론(THEN)의 두 부분으로 구성된다. 규칙의 전제 조건 이 일치하는 경우, 규칙은 점화되고 결론 부분이 실행된다.
- 규칙을 사용하는 시스템에는 작업 메모리라고도 하는 데이터베이스가 포함 된다. 작업 메모리에는 현재 관측된 사실이나 상태, 지식이 저장된다.
규칙 #1: IF 비가 온다. THEN 우산을 가져간다.
규칙 #2: IF 프로그램에 버그가 없다. THEN 프로그램은 올바르게 동작한다.
규칙 #3: IF 습도가 높다 OR 온도가 30도 이상이다. THEN 에어콘을 가동한다

의미망
- 의미망(semantic network)은 방향 그래프를 이용하여 개념 간의 관계를 나타 내는 방법이다.
- 그래프는 노드와 간선으로 이루어진다.
- 노드는 사물(objects), 개념(concepts)등을 표현한다.
- 간선(edge)는 사물이나 개념 사이의 관계이다.

- 노드 사이의 간선은 “..의 일종이다”(is-a), "...을 가지고 있다“('has), "...은 하 나의 예이다." (inst-of)와 같은 관계를 나타낸다.
- 의미망은 매우 복잡한 개념이나 인과 관계를 잘 표현할 수 있지만 지식의 양 이 커지면 너무 복잡해져서 조작이 어렵다는 단점도 가지고 있다.
- 의미망을 위한 표준 지침이 없기 때문에 시스템에 따라 의미망의 형태가 다를 수 있다.
프레임
- 프레임(frame)은 1970년대에 Marvin Minsky가 제안한 지식 표현 방법으로 의미망에서 파생
- 프레임은 특정 객체와 그 속성을 묶어서 하나로 조직화하는 방법이며 개념, 객체, 상황들을 기술하는데 유리하다.
책을 프레임으로 표현한 예
| 슬롯 | 값 |
| publisher | 인피니티북스 |
| title | 인공지능 |
| author | 홍길동 |
| edition | 초판 |
| year | 2019 |
| pages | 700 |
- 프레임은 객체의 속성과 값으로 이루어져 있다.
- 개개의 속성은 슬롯(slot)이라고 불리고 슬롯은 값을 가질 수가 있다.
- 프레임은 프로그래밍 언어의 구조체나 객체(object)와 유사하며 객체의 필드 에 해당하는 것은 슬롯이다.
컴퓨터를 프레임으로 표현한 예
| 슬롯 | 값 |
| name | 컴퓨터 |
| subclass | 기계 |
| types | default: desktop if-added: Procedure INCREMENT_COMPUTER |
| speed | default: fast if-needed: Procedure CALOULATE_SPEED |
프로시저
- “if-added” 프로시져는 새로운 정보가 그 슬롯에 추가되어야 할 때 실행된다.
- “if-deleted” 프로시져는 어떤 값이 슬롯으로부터 제거될 때 실행된다. 이 변경에 따라 다른 슬롯의 값도 변경할 필요가 있을 것이다.
- "if-needed" 프로시져는 빈 슬롯에 어떤 값이 필요해질 때에 실행된다.
프레임의 장점
- 개념을 구조화하여 표현할 수 있다. 프레임은 개념을 구조화하여 표현하기 때 문에, 개념과 개념 간의 관계, 속성, 기능 등을 명확하게 표현할 수 있다. 이로 인해 개념의 이해와 유추가 쉬워지며, 지식의 구성과 구조를 명확하게 파악할 수 있다.
- 지식의 재사용성이 높다. 프레임은 유사한 개념을 쉽게 만들 수 있기 때문에, 지식의 재사용성이 높다. 새로운 개념을 만들 때, 이미 만들어진 프레임을 조 합하여 새로운 프레임을 만들 수 있으며, 이를 통해 지식을 쉽게 확장할 수 있다.
- 지식의 일관성을 유지할 수 있다. 프레임은 개념을 구조화하여 표현하기 때문에, 개념 간의 관계와 속성이 일관성을 유지한다. 이로 인해 지식의 일관성을 유지할 수 있으며, 오류와 모순을 방지할 수 있다.
프레임과 객체 지향 프로그래밍
- 인공지능 분야에서는 프레임이란 용어로 객체를 나타낸다.
- 객체의 필드에 해당하는 것이 프레임의 슬롯이다.
- 프레임의 슬롯은 값뿐만 아니라 프로시저도 가질 수 있다. 슬롯에 붙은 프로시저가 바로 객체의 메소드라고 볼 수 있다.

프레임과 상속
- 프레임도 인스턴스 프레임(instance frame)과 클래스 프레임(class frame)으 로 나눌 수 있다.

시맨틱 웹
- Web Ontology Language(OWL)은 웹 상에서 지식 표현을 위한 규약으로, RDF(Resource Description Framework)와 함께 Semantic Web을 구현하는 데 사 용된다. OWL은 기존의 지식 표현 방법들과 달리, 웹 상에서 공유 가능한 지식 을 표현하고 검색할 수 있도록 설계되었다.
- OWL은 클래스, 속성, 인스턴스 등을 포함하는 객체 지향적인 구조를 가지며, 이들을 서로 연결하여 복잡한 지식 구조를 구성할 수 있다. 이를 통해, OWL을 이용하여 도메인의 개념과 속성, 그리고 개념 간의 관계를 정의할 수 있다.
- OWL은 프레임과 달리 객체 지향적인 표현 방법보다는, 논리적인 표현 방법을 중심으로 설계되어 있다. 따라서 OWL을 이용하면, 개념 간의 정확한 논리적 인 관계를 표현할 수 있다. 이러한 특징 때문에 OWL은 Semantic Web의 구현에 많이 활용되고 있다.
논리

술어논리
- 예를 들어보자. "만약 x가 새라면, x는 날개를 가질 것이다“라는 규칙이 있다고 하자.
(∀x) { is_a(x, Bird) → has(x, Wing)}
장점과 단점
• 수학적인 근거를 바탕으로 논리 개념을 자연스럽게 표현할 수 있 다.
• 지식의 정형화 영역에 적합하다. 예를 들어서 정리 증명(theorem proving) 기법을 사용할 수 있다.
• 지식의 첨가와 삭제가 용이하고 비교적 단순하다.
• 절차적인 지식 표현이 어렵다.
• 사실의 구성 법칙이 부족하므로 실세계의 복잡한 구조를 표현하기 어렵다.
명제논리
- 기호 논리학에서 명제(proposition)는 참(true, T)이거나 또는 거짓(false, F)을 판별할 수 있는 문장이다.
P = 마트는 월요일부터 토요일까지 영업한다.
Q = 오늘은 일요일이다.
R = 오늘 마트는 영업하지 않는다.
- 논리 연산자 사용 가능
Q = 오늘은 일요일이다.
NOT Q = 오늘은 일요일이 아니다.
J = 옷은 파랑색이다.
K = 옷은 스트라이프 무늬가 있다.
L = J AND K = 옷은 파랑색이고 스트라이프 무늬가 있다.
함축
C = 오늘은 휴일이다.
D = 오늘은 수업이 없다.
E = C → D
복합 명제의 논리표
| A | B | NOT A | A AND B | A OR B | A→B |
| T | T | F | T | T | T |
| T | F | F | F | T | F |
| F | T | T | F | T | T |
| F | F | T | F | F | T |
명제논리에서의 추론
- 추론(inference)이란 우리가 가지고 있는 지식과 우리가 이미 알고 있는 사실 로부터 새로운 사실을 유추하여 내는 것이다.
(지식) 우리집 강아지는 집안에 있거나 앞마당에 있다.
(사실) 강아지가 집안에 없다.
==============================================
(추론된 사실) 따라서 강아지는 앞마당에 있을 것이다.
추론법칙
- 모더스 포넌스(Modus Ponens)
규칙 | A → B
사실 | A
----------------
결론 B
"홍길동이 세계 일주 중이라면 → 로또에 당첨된 것이다. “
"홍길동은 세계 일주 중이다."
------------------------------------------------------
∴ ”홍길동은 로또에 당첨된 것이다."
- 부정 논법(Modus Tollens)
규칙 | A → B
사실 | NOT B
----------------
결론 NOT A
"어떤 동물이 강아지라면 → 어떤 동물은 4개의 다리를 가지고 있다.“
"어떤 동물은 4개의 다리를 가지고 있지 않다."
-------------------------------------------------------
∴ ”어떤 동물은 강아지가 아니다.“
- 삼단논법(syllogism)
규칙 | A → B
사실 | B → C
----------------
결론 A → C
“소크라테스는 인간이다”
“인간은 모두 죽는다”
-------------------------------------------------------
∴ “소크라테스는 죽는다”
술어논리
명제 논리에서 하나의 명제가 나누어질 수 없기 때문에 어려움이 있다. 즉 우리는 전체 명제가 참이냐 거짓이냐 만을 말할 수 있다.
예를 들어서 “신호등이 파랑색이다.”라는 명제가 있다면 이것을 “신호등”과 “파랑색이다”로 나눌 수 있다면 아주 편리할 것이다.
술어 논리에서는 하나의 명제가 객체(object, 또는 인수)와 술어(predicate)로 나누어진다.
변수와 한정자를 사용할 수 있다.
이와 같은 술어 논리의 특징 때문에 명제를 사용하는 것보다, 훨씬 더 구체적 으로 지식을 표현할 수 있다.
술어 논리의 예
명제 논리: Kim has a house
술어 논리: HAS(Kim, house)
명제 논리: The orange is yellow
술어 논리: YELLOW(orange)
객체와 관계
- 객체는 상수 기호로 나타낸다: 바둑이, 야옹이, Richard, ...
- 관계는 술어 기호로 나타낸다: HUMAN, DOG, CAT, HAT, ...

변수
- 예를 들어서 ”x가 인간이라면”은 다음과 같이 표현할 수 있다.
- HUMAN(x)
- x가 인간이라면 위의 술어 논리식은 참이 된다.
한정사
- 한정자는 변수의 범위를 서술하는 기호이다.
- 술어 논리에는 전칭 한정사(universal quantifier) ∀와 존재 한정사(existential quantifier) ∃를 사용할 수 있다.
- 전칭 한정사 ∀는 “모든” 이라는 의미이다.
- 존재 한정사 ∃는 “적어도 하나는 존재“한다는 의미이다.
All dog like cats
▼
∀x [DOG(x) → LIKES(x, cat)]
Some dogs like cats.
▼
∃x [DOG(x) → LIKES(x, cat)]
술어논리에서의 추론
- 첫 번째 방법은 술어 논리식을 명제 논리식으로 변환한 후에 명제 논리의 추론 기법을 적용하는 것
- 두번째 방법은 논리융합(resolution)이다.
정형식
- 우리가 논리융합을 사용하려면 모든 지식이 정형식(WFF: well-formed formula)으로 표현되어야 한다.
- 기초 공식은 정형식이다.
- P와 Q가 정형식이면 ¬P, P∨Q, P∧Q, P→Q도 정형식이다.
- P가 정형식이면 ∀x P(x) 와 ∃x P(x)도 정형식이다.
- 정형식은 위의 규칙을 반복하여서 형성가능하다.

논리융합
- 논리융합은 리터럴과 부정 리터럴을 가지고 있는 2개의 절을 조합하여서 새로운 절을 생성하는 방법이다.
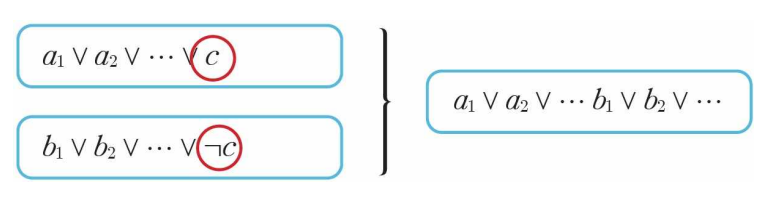
논리융합으로 모더스 포넌스를 유도해보자.

논리융합을 사용하려면
- 논리융합 기법으로 증명하려면 모든 논리식들을 논리곱 표준형(CNF: conjunctive normal form)으로 바꾸어야 한다.
- 모든 전칭 한정사는 없애버린다(기본적으로 가정된다).
- 존재 한정사는 스콜렘 함수라고 하는 것으로 바꾼다.
CNF로 변환하기
- 함축 기호 →를 제거한다.
- 부정 기호를 기초 공식 안으로 이동한다. 드모르간의 법칙을 이용하여 부정 의 범위를 줄인다.
- 전칭 한정사 변수의 이름을 다르게 변경한다.
- 존재 한정사에 의하여 한정되는 변수를 함수로 대체하고 존재 한정사를 제거한다.
- 모든 전칭 한정사를 생략하고, 논리곱 정규형으로 변환한다.
- 모든 논리곱 기호를 생략한다.
CNF로 변환하기 예
① 모든 강아지는 포유류이다.
② 바둑이는 강아지이다.
③ 바둑이는 포유류이다.
④ 모든 포유류는 우유를 생산한다.
▼ 술어논리로 변환
① ∀x (DOG(x) → MAMMAL(x)).
② DOG(badook).
③ MAMMAL(badook).
④ ∀x (MAMMAL(x) → MILK(x)).
▼ CNF로 변환
① ¬ DOG(x) ∨ MAMMAL(x)
② DOG(badook)
③ MAMMAL(badook)
④ ¬ MAMMAL(x) ∨ MILK(x)
논리융합에 의한 증명
1. 증명하고자 하는 사실을 부정하여 절들의 리스트에 추가한다.
2. 지식 베이스의 문장들을 CNF 형태로 변환한다.
3. 논리융합할 수 있는 절의 쌍이 더 이상 없을 때까지 다음을 반복한다.
3.1. 논리융합할 수 있는 절의 쌍을 찾아 논리융합한다.
3.2. 논리융합절을 절들의 리스트에 추가한다.
3.3. NIL이 유도되면, 증명하고자 하는 사실이 참이다.
4. 증명하고자 하는 사실이 거짓이다
논리융합에 의한 증명의 예
① ¬ DOG(x) ∨ MAMMAL(x)
② DOG(badook)
③ MAMMAL(badook)
④ ¬ MAMMAL(x) ∨ MILK(x)
MILK(badook)
▼
① ¬ DOG(x) ∨ MAMMAL(x)
② DOG(badook)
③ MAMMAL(badook)
④ ¬ MAMMAL(x) ∨ MILK(x)
⑤ ¬MILK(badook)

시맨틱 웹과 온톨로지 소개
기존 웹의 문제점
- 사람만 액세스할 수 있다는 점이다.
- 컴퓨터가 네트워크를 통해 정보를 전송받고 화면에 표시하지만, 올바른 정보를 선택하는 데 컴퓨터는 큰 도움이 되지 않는다.
- 예를 들어서 검색엔진이 발달하여서 사용자가 키워드를 입력하면 많은 검색 결과를 보여주지만, 아직은 사용자가 검색 결과를 클릭해서 내용을 읽기 전까지는 문서에 대한 정보를 올바르게 알 수 없다.
※ 그 이유는 무엇일까? 컴퓨터가 아직까지 웹 페이지의 구조와 레이아웃만 이해하고, 의미를 파악하지 못하기 때문이다.
시멘틱 웹
- 시맨틱 웹은 컴퓨터가 정보의 의미를 이해하고 추론할 수 있는 지능형 웹이 다. 웹 3.0이라고도 하는 시맨틱 웹(semantic web)은 W3C에서 설정한 표준 을 통해 웹을 확장한 것이다.
- 시맨틱 웹의 목표는 인터넷 상의 데이터를 컴퓨터들이 읽고 이해할 수 있도 록 만드는 것이다. 웹의 창시자 팀 버너스 리(Tim Berners Lee)는 1999년에 시맨틱 웹에 대한 자신의 비전을 다음과 같이 표현했다.
시멘틱 웹의 예
홍길동은
서울
에서 태어났다.
시멘틱 웹의 요소 기술
- 웹 자원을 서술하기 위한 RDF(Resource Description Frame)
- 온톨로지(Ontology)
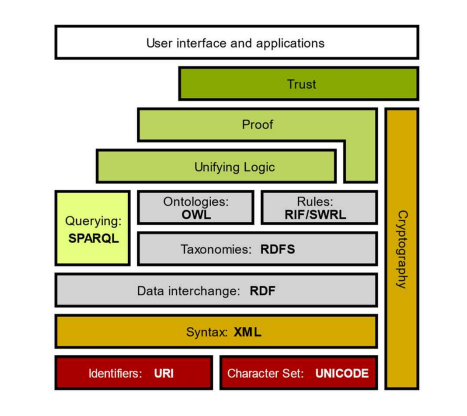
온톨로지
- 컴퓨터 과학에서 온톨로지는 지식공학 분야에서 사용되는 지식 표현 방법 중 하나이다. 온톨로지는 인공지능 분야에서 개념의 의미와 관계를 정의하는 데 사용되며, 지식을 표현하는 방법 중 하나이다.
- 온톨로지는 일종의 분류체계를 만들어내며, 개념, 속성, 관계, 제약 등의 정보 를 포함한다. 이러한 정보는 자연어로 기술된 경우 다양한 해석이 가능하므로, 온톨로지를 이용하여 명확하고 일관된 의미를 부여할 수 있다.
- Individuals(instance): 사람, 동물, 책상, 자동차, 분자, 행성 등의 구체적 객체(objects)
- Classes: object의 type
- Attributes: object의 속성
- Relations: object가 다른 object와 연관되는 방법
온톨로지의 예
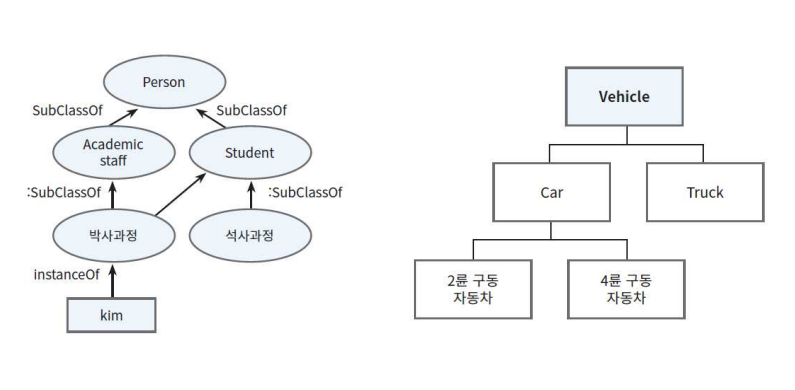
논리융합 연습
- 간단한 논리융합 연습을 해보자. 다음과 같은 지식이 있다.
① 어떤 것이 지능적이라면 그것은 상식을 가져야 한다.
② PC는 상식이 없다.
- 위의 지식을 바탕으로 PC는 지능적이 아니다를 증명해 보자.

요약
- 많이 사용되는 지식 표현의 방법은 “규칙”, “의미망”, “프레임”, 술어논리 “ 등이 있다.
- 명제 논리에서 추론 방법은 “모더스 포넌스”, “부정 논법”, “삼단논법” 등이 있다.
- 의미망(semantic network)은 방향 그래프를 이용하여 개념 간의 관계를 나타내는 방법이다.
- 프레임(frame)은 1970년대에 Marvin Minsky가 제안한 지식 표현 방법으로 특정 객체와 그 속성을 묶어서 하나로 조직화하는 방법이다.
- 술어 논리(predicate logic)는 하나의 명제가 객체(object, 또는 인수)와 술어 (predicate)로 나누어질 수 있고 변수와 한정자를 사용할 수 있는 논리이다.
- 술어 논리식에서는 추론을 위하여 논리융합(resolution)이라는 방법을 사용 한다.
728x90
반응형
'끝이없는 공부 > 인공지능개론' 카테고리의 다른 글
| [인공지능개론] 6장. 퍼지논리 (1) | 2024.05.08 |
|---|---|
| [인공지능개론] 4장. 전문가시스템 (0) | 2024.05.01 |
| [인공지능개론] 3장. 게임트리 (2) | 2024.04.27 |
| [인공지능개론] 2장. 탐색 (0) | 2024.04.19 |
| [인공지능개론] 1장. 인공지능 소개 (0) | 2024.04.19 |



