[인공지능개론] 1장. 인공지능 소개
▶인공지능의 의미를 이해한다. ▶지능의 특징을 살펴본다. ▶튜링 테스트를 이해한다. ▶인공지능이 사용되는 분야를 이해한다. ▶인공지능의 역사를 이해한다. ▶파이썬을 설치한다. 알파고
bluedayj.tistory.com
▶ 탐색의 개념을 소개
▶ 상태, 상태 공간, 연산자의 개념을 소개
알파고는 어떻게 수를 읽었을까?
알파고는 딥러닝과 탐색 기법을 통하여 다음 수를 읽었다.

상태, 상태공간, 연산자
- 탐색(search)이란 상태공간에서 시작상태에서 목표상태까지의 경로를 찾는 것
- 상태공간(state space): 상태들이 모여 있는 공간
- 연산자: 다음 상태를 생성하는 것
- 초기상태
- 목표상태

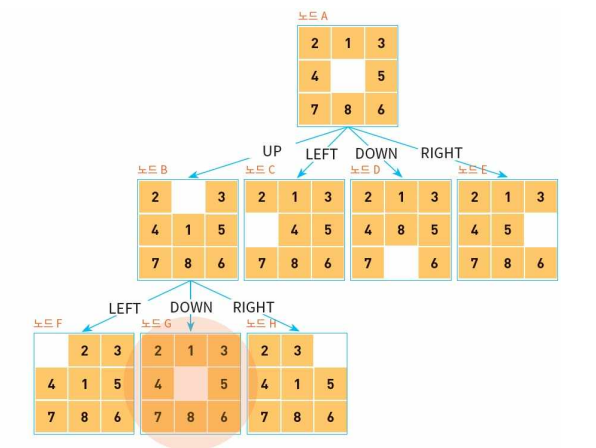
8-퍼즐
8-퍼즐은 슬라이딩 퍼즐의 일종으로, 타일을 움직여서 순서대로 맞추는 퍼즐 놀이입니다.

8-퍼즐에서의 연산자 빈칸을 4방향으로 움직이는 UP, DOWN, LEFT, RIGHT입니다.

8-퍼즐에서의 연산자

8-퍼즐에서의 상태 공간

경로 찾기 문제
- 탐색의 대표적인 문제 중의 하나가 경로를 찾는 문제이다. 예를 들어서 다음 과 같이 도시들이 연결되어 있다고 하자.
- 상태?
- 연산자?
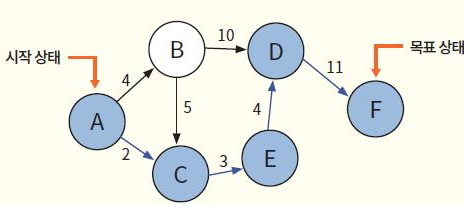
- 이 문제에서 초기 상태, 목표 상태, 연산자 등을 생각해보자.
- 초기 상태는 에이전트가 A에 있는 것이다.
- 목표 상태는 에이전트가 F에 있는 것이다.
- 연산자는 가능한 경로 중에서 하나의 경로를 선택하는 것이다
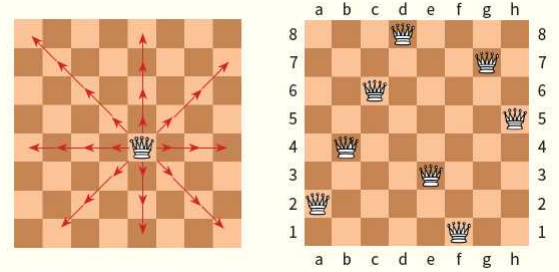
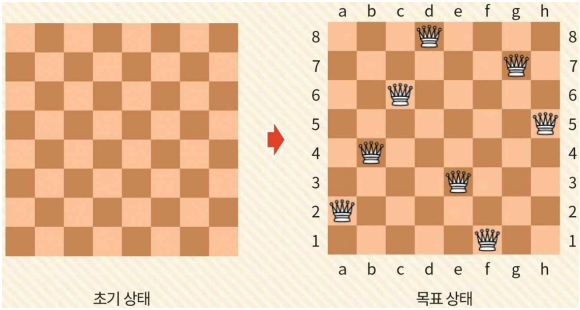
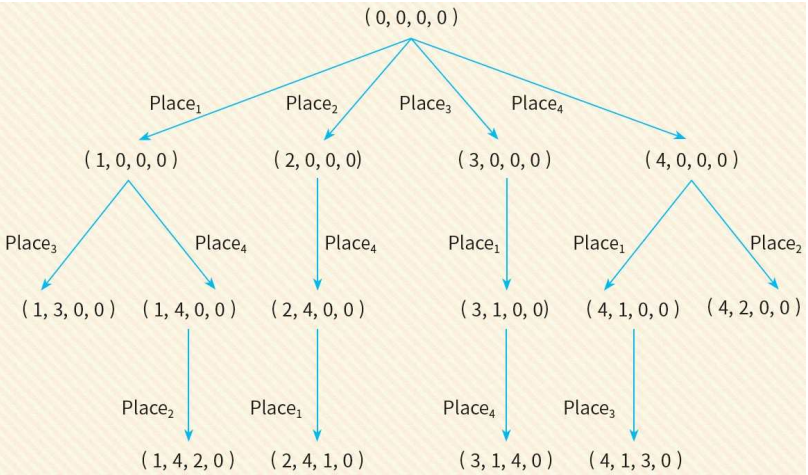
N-queen
- 8-queen 문제는 8×8 체스판에 두 개의 퀸이 서로를 위협하지 않도록 8개의 퀸을 배치하는 문제이다.
- 상태?
- 연산자?
- 각각의 퀸을 정해진 열에서만 움직이게 한다.
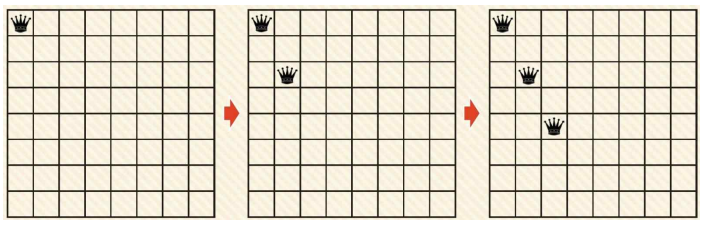
초기 상태와 목표 상태
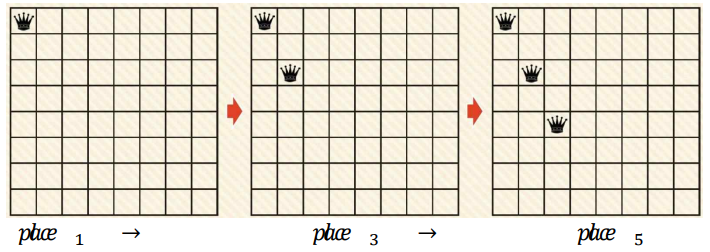
- 연산자 집합 O = { place i | i <= i <= 8}
- place i 연산자는 새로운 퀸을 i번째 행에 배치한다.
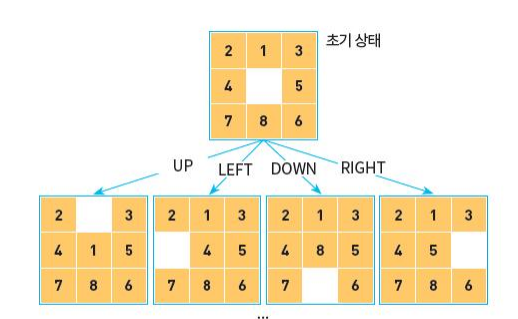
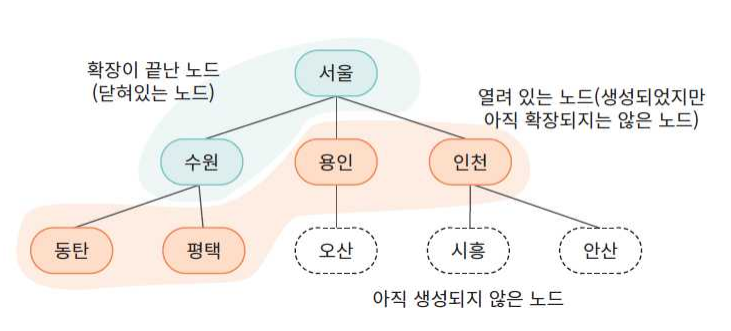
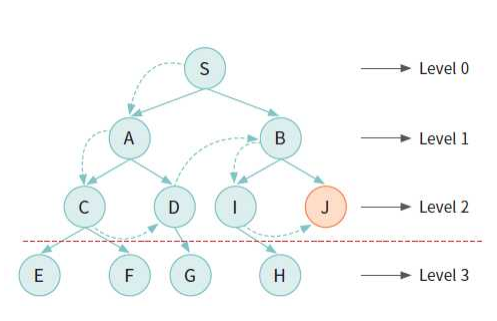
탐색트리
- 상태 = 노드(node)
- 초기 상태 = 루트 노드
- 연산자 = 간선(edge
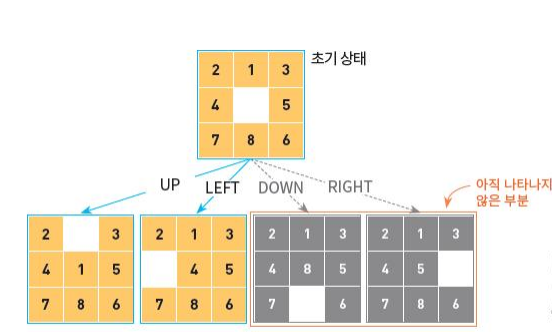
- 연산자를 적용하기 전까지는 탐색 트리는 미리 만들어져 있지 않음
탐색 트리의 예
다음 그림은 출발 도시에서 목표 도시까지의 경로를 탐색하는 문제에서 노 드들을 분류하였다.
4-queen 문제 탐색 트리의 일부
기본적인 탐색 기법
탐색 알고리즘
맹목적인 탐색
- 깊이 우선 탐색
- 너비 우선 탐색
- 균일 비용 탐색
경험적인 탐색
- 탐욕적인 탐색
- A*탐색
맹목적인 탐색 vs 경험적인 탐색
- 맹목적인 탐색 방법(blind search method)은 목표 노드에 대한 정보를 이용 하지 않고 기계적인 순서로 노드를 확장하는 방법으로 매우 소모적인 탐색 을 하게 된다.
- 경험적 탐색 방법(heuristic search method)은 목표 노드에 대한 경험적인 정보를 사용하는 방법이다. 따라서 효율적인 탐색이 가능하다. 이런 경험적 인 정보를 휴리스틱(heuristic)이라고 한다.
탐색 성능 측정
- 완결성(completeness): 문제에 해답이 있다면, 반드시 해답을 찾을 수 있는 지 여부
- 최적성(optimality): 가장 비용이 낮은 해답을 찾을 수 있는지 여부
- 시간 복잡도(time complexity): 해답을 찾는데 걸리는 시간
- 공간 복잡도(space complexity): 탐색을 수행하는 데 필요한 메모리의 양
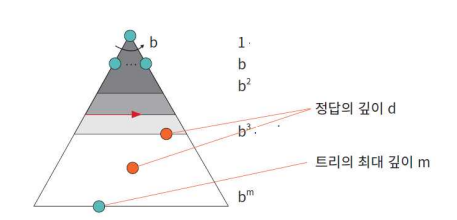
- b: 탐색 트리의 최대 분기 계수
- d: 목표 노드의 깊이 § m: 트리의 최대 깊이
깊이 우선 탐색(DFS)
깊이 우선 탐색(depth-first search)은 탐색 트리 상에서, 해가 존재할 가능 성이 존재하는 한, 앞으로 계속 전진하여 탐색하는 방법
깊이 우선 탐색(8-puzzle)
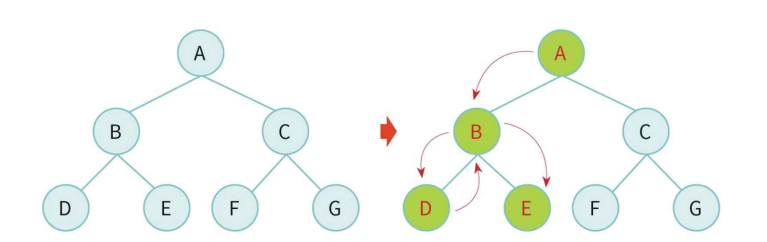
OPEN 리스트와 CLOSED 리스트
탐색에서는 중복된 상태를 막기 위하여 다음과 같은 2개의 리스트를 사용한다.
- OPEN 리스트: 확장은 되었으나 아직 탐색하지 않은 상태들이 들어 있는 리스트
- CLOSED 리스트: 탐색이 끝난 상태들이 들어 있는 리스트
DFS 예
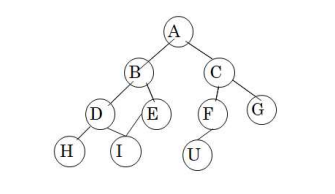
open = [A]; closed = []
open = [B,C]; closed = [A]
open = [D,E,C]; closed = [B,A]
open = [H,I,E,C]; closed = [D,B,A]
open = [I,E,C]; closed = [H,D,B,A]
open = [E,C]; closed = [I,H,D,B,A]
open = [C], closed = [E,I,H,D,B,A] (I는 이미 close 리스트에 있으니 추가되지 않는다.)
open = [F,G]; closed = [C,E,I,H,D,B,A]
open = [U,G]; closed = [F,C,E,I,H,D,B,A]
목표 노드 U 발견!
깊이 우선 탐색의 분석
- 완결성: 무한 상태 공간에서는 깊이 우선 탁색은 무한 경로를 따라 끝없이 나갈 수 있다. 따라서 무한 상태 공간에서는 완결적이지 않다.
- 시간 복잡도: O(b^m)이다. 여기서 b는 분기 계수이다. 만약 m(트리의 최대 깊이)이 d(정답의 깊이)보다 아주 크다면 시간이 많이 걸린다. 그렇지 않은 경우에는 너비 우선 탐색보다도 빠를 수 있다.
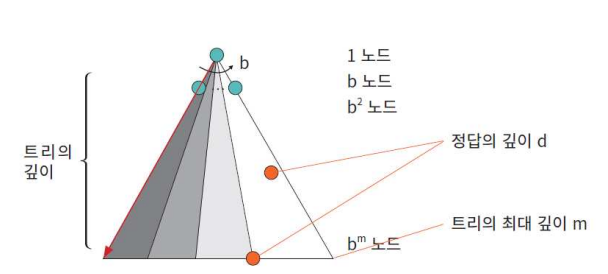
- 공간 복잡도: O(bm), 즉, 선형 복잡도만을 가진다. 탐색 트리에서 한 줄 단 위로 탐색하므로 모든 노드를 저장하고 있을 필요는 없다. 이점은 너비 우선 탐색에 비하여 큰 장점이다. 만약 b가 10이고, 노드당 1KB가 필요하다고 하 자, 만약 m=10이라고 하면 100KB 바이트만 필요하다. 만약 너비 우선 탐색 이라면 10TB가 필요하다.
- 최적성: 가장 경로가 짧은 최적의 해답은 발견할 수 없다. 가장 왼쪽 (leftmost)에 있는 해답만을 발견한다.
너비 우선 탐색(BFS)
루트 노드의 모든 자식 노드들을 탐색한 후에 해가 발견되지 않으면 한 레벨 내려가서 동일한 방법으로 탐색을 계속하는 방법이다.
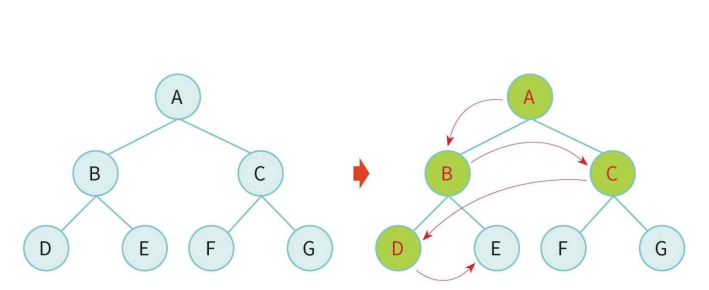
BFS 예

open = [A]; closed = []
open = [B,C]; closed = [A]
open = [C,D,E]; closed = [B,A]
open = [D,E,F,G]; closed = [C,B,A]
open = [E,F,G,H,I]; closed = [D,C,B,A]
open = [F,G,H,I], closed = [E,D,C,B,A] (I는 이미 close 리스트에 있으니 추가되지 않는다.)
open = [G,H,I,U]; closed = [F,E,D,C,B,A]
open = [H,I,U]; closed = [G,F,E,D,C,B,A]
open = [I,U]; closed = [H,G,F,E,D,C,B,A]
open = [U]; closed = [I,H,G,F,E,D,C,B,A]
목표 노드 U 발견!
너비 우선 탐색의 분석
- 완결성: 분기 계수 b가 유한하면 너비 우선 탐색은 반드시 해답을 발견할 수 있다.
- 시간 복잡도와 공간 복잡도: 일단 생성되는 노드의 개수를 세어보자. 이 노드들이 메모리 상에 있어야 하므로 시간 복잡도와 공간 복잡도는 모두 지수 복잡도 O(b^d ) 가 된다. 시간 복잡도보다도 공간 복잡도가 더 문제이다. 분기 계수가 10이고, 깊이 10까지만 탐색한다고 하자. 한 개의 노드를 저장하는 데 1KB가 든다면 메모리는 최대 =10TB가 필요하게 된다. 아주 간단한 문제 가 아니라면 천문학적인 시간과 메모리 공간이 필요하다고 할 수 있다.
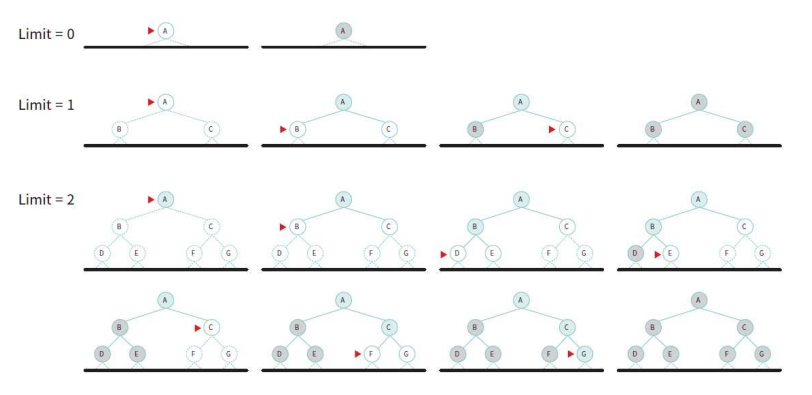
깊이 제한 탐색
깊이 우선 탐색(DFS)은 메모리 소모도 적고 정답을 빠르게 찾을 수도 있지만, 한번 잘못된 경로로 빠지면 나오지 못할 수도 있다. 이 단점을 보완한 것이 깊이를 제한하는 ‘깊이 제한 탐색(Deep-Limited Search)’이다. DFS와 기본 적인 것은 같지만, 끝까지 깊이 들어가지 않고 어떤 한계를 정해서 그 깊이 이상은 탐색하지 않고 백트랙킹하는 것이다.
IDDFS(Iterative Deepening DFS)
한계 깊이를 1, 2, 3, 4 ... 이렇게 차례대로 늘려가며 깊이 제한 탐색을 진행 하는 것이다. 목표를 찾을 때까지 제한 깊이를 늘려가면서 탐색한다.
IDDFS의 특징
- IDDFS는 깊이 우선 탐색의 공간 효율성과 너비 우선 탐색의 완전성을 결합 한다. 또 해답이 존재하는 경우, 가장 적은 비용을 갖는 경로를 찾는다. IDDFS이 여러 번 동일한 노드를 방문하기 때문에 낭비처럼 보일 수 있지만, 탐색 트리에서는 대부분의 노드가 하위 수준에 있기 때문에 비용이 생각보다 많이 들지 않는다.
- 알고리즘의 응답성이 향상된다. 초기 반복에서는 작은 수의 노드를 사용하 기 때문에 매우 빠르게 실행된다. 알고리즘은 초기 결과를 빠르게 제공할 수 있다. 따라서 프로그램이 지금까지 완료한 탐색에서 찾은 최고의 결과로 언 제든지 작업을 수행할 수 있다.
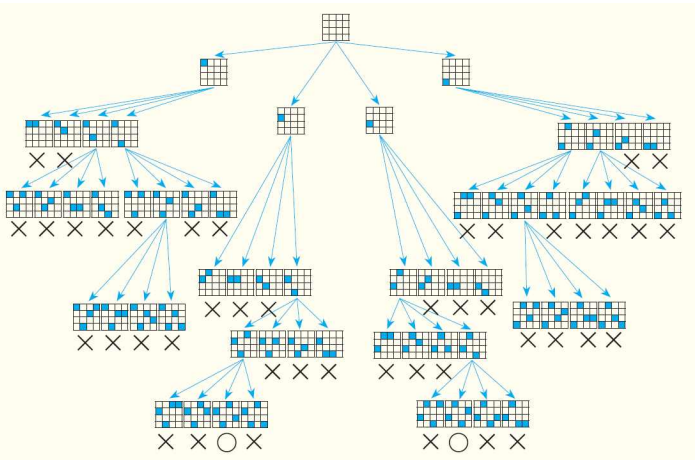
N-queen 문제에서 맹목적 탐색
일단 문제를 간단하게 하기 위하여 하나의 퀸이 하나의 열에서만 움직인다 고 가정하자. 하나의 열을 하나의 퀸이 장악하고 있다고 생각하자.
경험적인 탐색 방법
- 만약 우리가 문제 영역에 대한 정보나 지식을 사용할 수 있다면 탐색 작업을 훨씬 빠르게 할 수 있다. 이것을 경험적 탐색 방법(heuristic search method) 또는 휴리스틱 탐색 방법이라고 부른다.
- 이때 사용되는 정보를 휴리스틱 정보(heuristic information)라고 한다.
8-puzzle에서의 휴리스틱
언덕 등반 기법
경험적인 탐색 방법은 무조건 휴리스틱 함수 값이 가장 좋은 노드만을 선택 한다.
이것은 등산할 때 무조건 현재의 위치보다 높은 위치로만 이동하는 것과 같다. 일반적으로는 현재의 위치보다 높은 위치로 이동하면 산의 정상에 도달 할 수 있다.
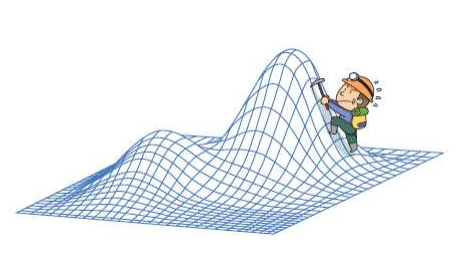
지역 최소 문제
- 순수한 언덕 등반 기법은 오직 h(n) 값만을 사용한다(OPEN 리스트나 CLOSED 리스트도 사용하지 않는다).
- 이런 경우에는 생성된 자식 노드의 평가함수 값이 부모 노드보다 더 높거나 같은 경우가 나올 수 있다. 이것을 지역 최소 문제(local minima problem)라 고 한다.
지역 최소 문제의 예
A* 알고리즘
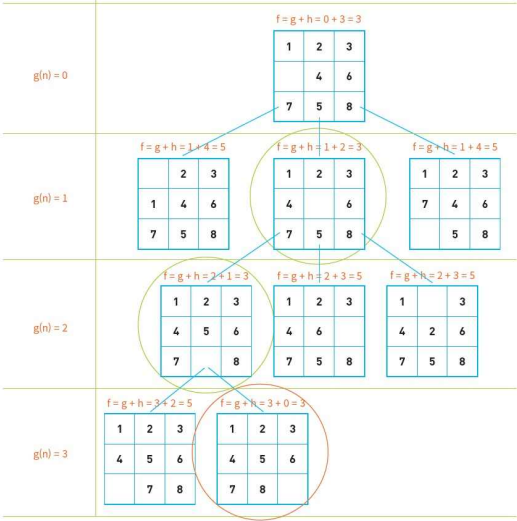
A* 알고리즘은 평가 함수의 값을 다음과 같은 수식으로 정의한다. f(n) = g(n) + h(n)
- h(n): 현재 노드에서 목표 노드까지의 거리
- g(n): 시작 노드에서 현재 노드까지의 비용
8-puzzle에서의 A* 알고리즘
요약
- 탐색은 상태 공간에서 시작 상태에서 목표 상태까지의 경로를 찾는 것이다. 연산자는 하나의 상태를 다른 상태로 변경한다.
- 맹목적인 탐색 방법(blind search method)은 목표 노드에 대한 정보를 이용 하지 않고 기계적인 순서로 노드를 확장하는 방법이다. 깊이 우선 탐색과 너 비 우선 탐색이 있다.
- 탐색에서는 중복된 상태를 막기 위하여 OPEN 리스트와 CLOSED 리스트를 사용한다.
- 경험적 탐색 방법(heuristic search method)은 목표 노드에 대한 경험적인 정보를 사용하는 방법이다. “언덕 등반 기법” 탐색과 A* 탐색이 있다.
- A* 알고리즘은 f(n) = g(n) + h(n)으로 생각한다. h(n): 현재 노드에서 목표 노드까지의 거리이고 g(n): 시작 노드에서 현재 노드까지의 비용이다.
'끝이없는 공부 > 인공지능개론' 카테고리의 다른 글
| [인공지능개론] 6장. 퍼지논리 (1) | 2024.05.08 |
|---|---|
| [인공지능개론] 5장. 지식표현 (0) | 2024.05.07 |
| [인공지능개론] 4장. 전문가시스템 (0) | 2024.05.01 |
| [인공지능개론] 3장. 게임트리 (2) | 2024.04.27 |
| [인공지능개론] 1장. 인공지능 소개 (0) | 2024.04.19 |



